Triangles and its properties

Properties:


Exterior angle and its property:


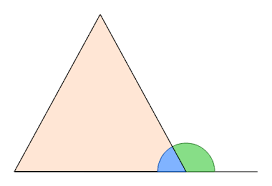
What is an exterior angle?

An exterior (or external) angle is the angle between one side of a triangle and the extension of an adjacent side.

The angle in green colour is Exterior angle.

Exterior angle property:

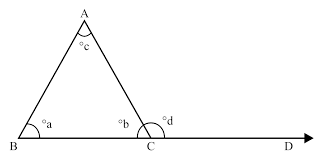
An exterior angle of a triangle is equal to the sum of the opposite interior angles.

In the above figure exterior angle is d

According exterior angle property,d=a+c


Exterior Angle Theorem:

Consider ∆ABC. 

 ∠ACD is an exterior angle.
     	To Show: ∠ACD = ∠A + ∠B
        Through C draw CE, parallel to BA

Justification:

S.no Steps Reasons
1. ∠1 = ∠x BA || CE and AC is a transversal. Therefore, alternate angles should be equal
2. ∠2 = ∠y BA || CE and BD is a transversal.
3. ∠1 + ∠2 = ∠x + ∠y From step-1 and step-2
4. ∠1 + ∠2 = ∠x + ∠y From the figure above.
5. ∠1 + ∠2 = ∠ACD From step-3 and step-4

The above relation between an exterior angle and its two interior opposite angles is referred to as the Exterior Angle Property of a triangle.

Angle sum property:

The angle sum property of a triangle:The total measure of the three angles of a triangle is 180 °

From the above figure ,x+y+z=180 °

proof:

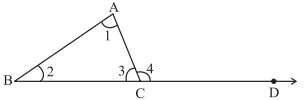
To justify this let us use the exterior angle property of a triangle. Given : ∠1, ∠2, ∠3 are angles of ΔABC. ∠4 is the exterior angle when BC is extended to D.

Justification:

     ∠1 + ∠2 = ∠4 (by exterior angle property) 
     ∠1 + ∠2 + ∠3 = ∠4 + ∠3 (adding ∠3 to both the sides). 
     But ∠4 and ∠3 form a linear pair so it is 180°. 
     Therefore, ∠1 + ∠2 + ∠3 = 180.

Example1:

Given that In a triangle, the two interior angles are 35 °and 60 ° are non adjacent to exterior angle x°. Find x.

     Apply the Triangle exterior angle theorem:
  that is,        x °=35 °+60 °
                  x °=95 °

Example2:

In the Δ ABC, x=55 °,y=55 ° , find the angle z °?

 In Δ ABC,
    x + y + z= 180 °
                  [By angle sum property of a triangle]

=> 55 ° + 55 ° + z °= 180 °
=> 110 ° + z ° =  180 °
=> z ° = 70 °