operation of stets
We know that arithmetic has operations of additions, subtraction and multiplication of
numbers. Similarly in sets, we define the operation of union, intersection and difference of sets.
Union of sets:
In set theory, the union of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other.
A nullary union refers to a union of zero sets and it is by definition equal to the empty set.
Example-1:
Let A = {2, 5, 6, 8} and B = {5, 7, 9, 1}. Find A ∪ B.
Solution:
We have A ∪ B = {1, 2, 5, 6, 7, 8, 9}.
Note that the common element 5 was taken only once while writing A ∪ B.
Example-2:
Let A = {a, e, i, o, u} and B = {a, i, u}. Show that A ∪ B = A.
Solution:
We have A ∪ B = {a, e, i, o, u} = A.
This example illustrates that union of sets A and its subset B is the Set A itself
i.e, if B ⊂ A, then A ∪ B = A.
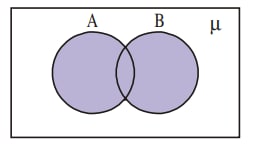
The union of the sets can be represented by a Venn-diagram as shown (shaded portion)
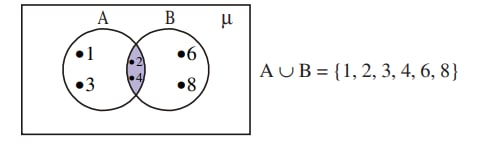
Example-3:
Illustrate A ∪ B in Venn-diagrams where
A = {1, 2, 3, 4} and B = {2, 4, 6, 8}
Solution