LEAST COMMON MULTIPLES
Common Multiples:
Example
The multiples of 4 and 6 are
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, ....., ....., .....
Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, ....., ....., .....
Common multiples of both 4 and 6 = 12, 24, 36, ....., ....., .....
Definition:
The least common multiple of two or more given numbers is the lowest (or smallest or least) of their common multiples. Methods of Finding LCM
- Prime Factorization Method
- Division Method
The LCM of 36 and 60 can be found by prime factorization method as follows:-
Step-1:
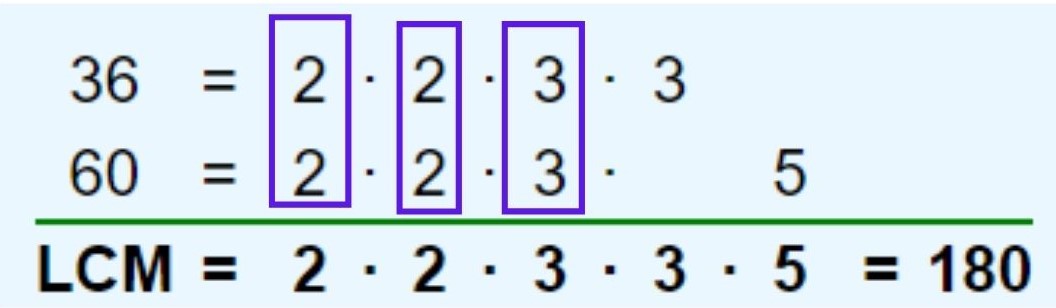
Factors of 36 = 2 * 2 * 3 * 3
Factors of 60 = 2 * 2 * 3 * 5
Step-2:Take the common factors of both: 2 * 2 * 3
Step-3:Take the extra factors of both 36 and 60 i.e. 3 and 5.
Step-4:LCM is found by the product of all common prime factors of two numbers and extra prime factors of both.
Hence, the LCM of 36 and 60 = (2 * 2 * 3 )* 3 * 5 = 180
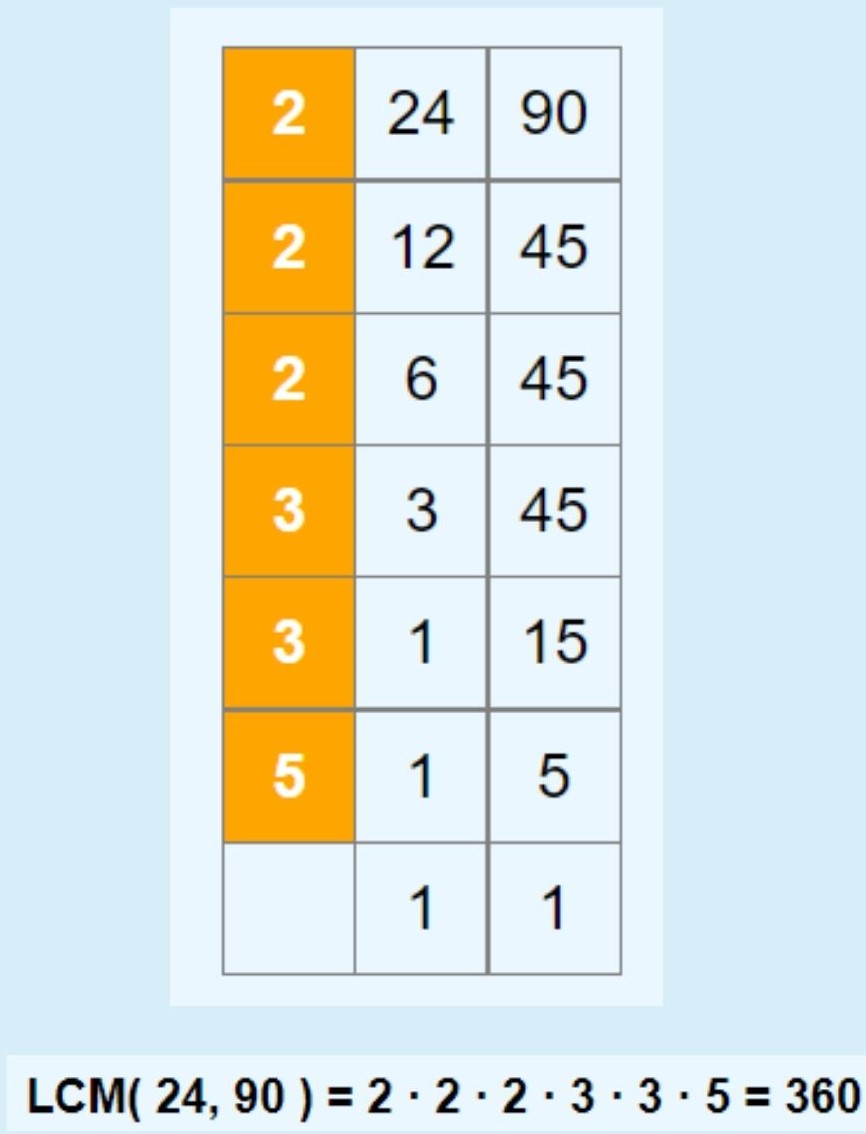
To find the LCM of 24 and 90:
Step-1:Arrange the given numbers in a row.
Step-2:Then divide by a least prime number which divides at least two of the given numbers
and carry forward the numbers which are not divisible by that number if any.
Step-3:Repeat the process till no numbers have a common factor other than 1.
Step-4:LCM is the product of the divisors and the remaining numbers.
Thus, the LCM of 24 and 90 is 2 * 3 * 4 * 15 = 360
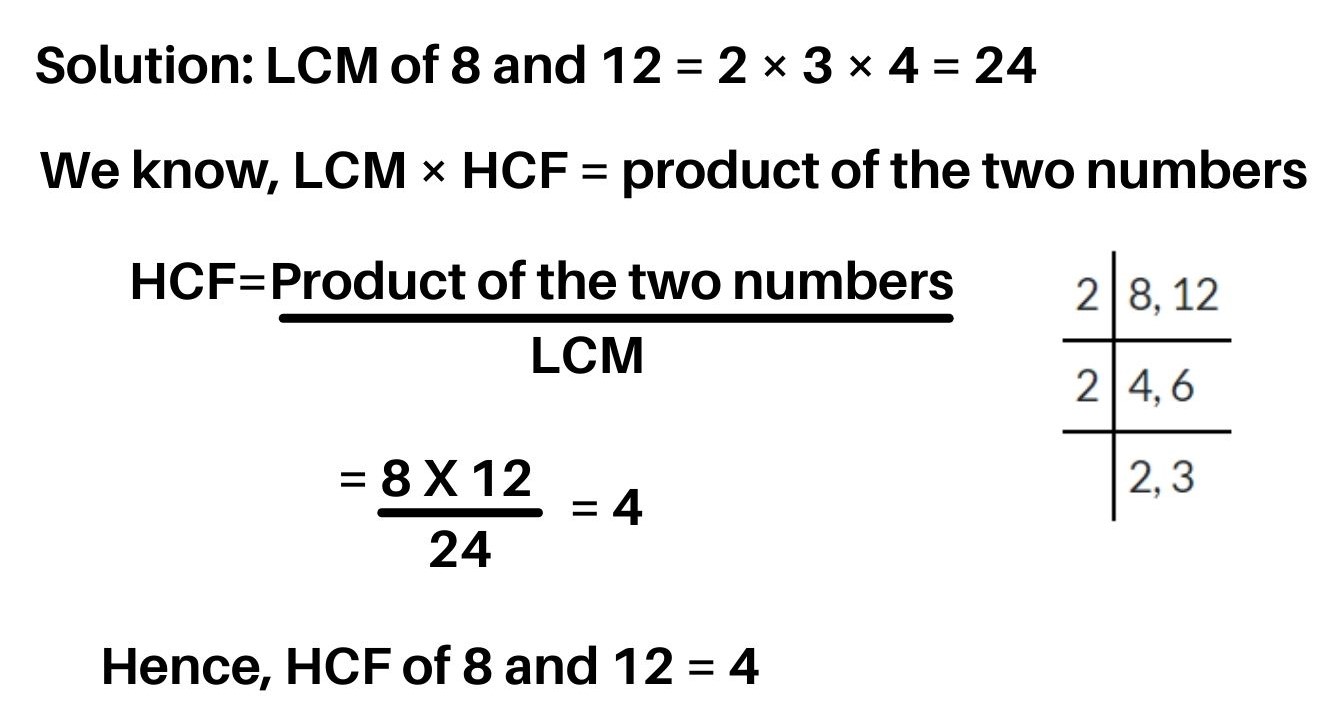
The product of Highest Common Factor(HCF) and Least Common Multiple(LCM) of two numbers is equal to the product of two numbers

1. Find the LCM of 21, 35 and 42.
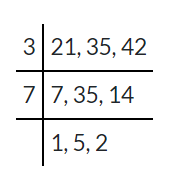
So the LCM of the given numbers is 3 x 7 x 1 x 5 x 2 = 210
2. Find the LCM of 8 and 12 and then find their HCF using the relation formula.
DO YOU KNOW?
- The smallest number which is exactly divisible by a, b and c is L.C.M of a, b, c.
- The L.C.M of two or more numbers is greater than or equal to the greatest number of given numbers.
- If one of the two given numbers is a multiple of the other, then the greater number is the LCM of the given numbers.
Can you try this?


